quinta-feira, 10 de fevereiro de 2011
EMPRÉSTIMO PESSOAL OU AUTOMÁTICO?
Na minha infância e, antes de entrar na escola, os meus pais me ensinaram a fazer as quatro operações fundamentais, ou seja:
soma, subtração, multiplicação e a divisão.
A subtração me foi ensinada pelo método de complementação que era usado na época (epa! Não sou do tempo do dilúvio universal... embora tenha pisado na lama dele! Rsrsrsrsrs!) e que continuou em uso, até que surgiu a tal da “Matemática Moderna” quando esse método para se fazer a subtração, foi abandonado e substituído pelo método do “Tomar Emprestado”, que é o usado atualmente.
Nada tenho contra o tal método, quanto a sua eficácia nos resultados.
Nada tenho contra o tal método, quanto a sua eficácia nos resultados.
Mas, se compararmos com a rapidez, permanência intocada da escrita do minuendo e verificação (prova real da subtração) do método anterior, ele perde feio!
Eu tenho, ensinado esse método “antigo” para os meus alunos e eles ficam surpresos com o mesmo e, muitas vezes já aconteceu de brigarem com os seus mestres (que também, não sabiam do método) para utilizarem o “Empréstimo Automático” ou o método do... “Para”, como alguns já o rebatizaram.
Também, muitos amigos meus professores, já aderiram ao método, depois que lhes faço a demonstração.
Enfim... questão de gosto não se discute, cada um tem uma razão para escolher o seu, portanto, farei aqui e agora a demonstração do método da “complementação “ para a operação da subtração.
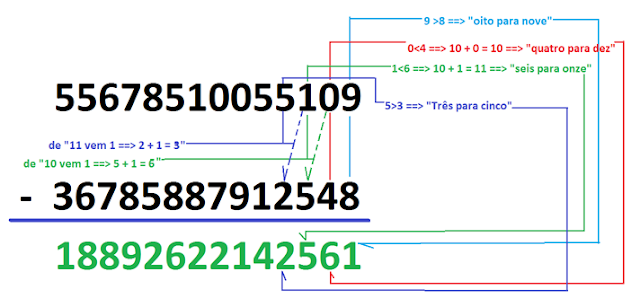
Sejam os números: 55678510055104 (minuendo) e 36785887912048 (subtraendo) e queremos achar a diferença entre eles, assim...
55678510055109
-36785887912548
____________________
O método da complementação, consiste em somarmos 10 unidades ao número representado por um dígito do minuendo (o termo de cima) se ele for menor que o número correspondente ao dígito no subtraendo (o termo de baixo) na sua mesma posição ou ordem.
Sabemos que a subtração se faz a partir da direita para a esquerda e uma vez que a conta está armada, como no nosso exemplo, então começamos pela ordem das unidades:
9 – 8 = 1. Lê-se: “nove menos oito” e aqui, para funcionar como um mnemônico, diremos... “oito para nove” ou seja: o complementar de oito em relação ao nove é 1, ou ainda: aquilo que falta ao oito para que seja igual a nove são... uma unidade!
E assim a complementação na ordem das unidades simples, já está resolvida. Passamos para a próxima a próxima ordem, a das dezenas...
como 0 – 4 “zero menos quatro” não pode (pelo método do “empréstimo” atual, tomar-se-ia uma dezena emprestada na ordem das centenas) então, pelo que eu já dissera antes, como o “zero é menor do que o quatro” então pelo “empréstimo automático”, somamos 10 unidades ao 0 (zero) … o que dá 10 e fazemos... “quatro para dez” ou 10 – 4 = 6, como pomos verificar aqui...
55678510055109
-36785887912548
____________________
61
mas, agora, preste bastante atenção, pois quando um valor no minuendo é igual a: “dez”, “onze”, “doze”... até o “dezenove” no minuendo, o termo de cima, o valor 1 no início em cada um deles (ordem das dezenas) vai ser somado com o valor do número embaixo no subtraendo na próxima ordem.
Feito isso, é só repetirmos o procedimento anterior, o que no nosso exemplo temos até agora: “oito para nove” dá 1, “quatro para dez” dá 6, de “dez vem um... soma com o cinco, dá seis” e “seis para onze” (já sabe porque, relembrando: 1 < 6 ==> 10 + 1 = 11) é igual a 5, como podemos ver...
55678510055109
-36785887912548
____________________
561
e prosseguiremos agora, através do uso de imagens:
********************************************************************










































6 comentários:
Olá Francisco, me chamo Saraí, sou professora de matemática e estou em busca de bibiliografia que possam me ajudar a entender o método de subtração por complementação, que você dispõe aqui no blog.
16 de julho de 2011 às 09:12Teria algo que pudesse me indicar? Inclusive ,você cita que esse era um método utilizado antes do moviemento matemática moderna? Onde posso buscar embasamento para essa referência?
Aguardo contato e desde já agradeço pela atenção dispensada
sarai.os@ig.com.br
Olá, profª Saraí!
17 de julho de 2011 às 06:27Fico muito honrado com a sua presença em meu blog, sendo uma seguidora também e ainda interessada pelas "velharias" que funcionam!
Infelizmente, professora Saraí... não conheço aonde se possa encontrar material disponível sobre esse método, além da minha postagem. Mas, estarei à vossa disposição para lhe prestar outros exemplos que queira, bastando que escreva para... franciscovaldir61@gmail.com e lhe atenderei com prazer!
Muita paz e saúde! até breve!
Um abraço!!!!!
Professor Francisco, antes de mais nada preciso parabenizá-lo pelo Blog, um trabalho que disponibilizar para todos, conhecimentos e saberes que muitas vezes não encontramos nos livros em voga.Isso sem contar com a possibilidade de troca a partir de um tópico abordado. Parabéns mesmo. Quando você fala em "velharia" me leva a pensar no quão significativo era o aprendizado de outrora. Hoje numa concepção de que aprender significa dominar técnicas, mesmo que não consiga compreendê-las ou mesmo entender o que as valida, velharias são recursos cada vez mais solicitados por aqueles que buscam fazer a diferença. Isso já dizia Piaget!
17 de julho de 2011 às 07:48Abraço!
Olá, profª Saraí!
17 de julho de 2011 às 09:22Muito obrigado, pelos elogios tão carinhosos!
Concordo contigo, pois... "esqueça o passado e... terás dispensado o melhor dos teus mestres"! Não sei se inventei ou li isso, mas uma "coisa" (conhecimento) por ser velha, poderá ser a peça crucial para alavancar a modernidade!
Estarei à vossa disposição, então... até breve!
Um abraço!!!!!
Nao sou professor de matematica
13 de julho de 2012 às 12:34Li o seu texto, mas nao compreendi.
Mas vou comentar como ensinei minha filha a fazer
conta de subtração sem usar o "pede 1 para o vizinho".
Um exemplo:
71
-47
----
ensinei ela a pegar o 47 e descobrir quanto
falta para chegar a 50
depois quanto falta chegar do 50 ao 60
(que é fácil por ser dezena)
depois do 60 para o 70
e por fim do 70 para o 71
e representei no papel assim:
47____50____60____70___71
3 10 10 1
depois
basta somar os valores encontrados:
3
10
10
1
==
24
Ela aprendeu e eu achei mais facil
do que o metodo de "pedir 1 para o vizinho".
A minha duvida é:
estou errado em ensinar ela pelo metodo que expliquei acima ?
Quais seus comentarios ?
Olá, Palavras!!!!
13 de julho de 2012 às 13:50Em primeiro lugar, quero agradecer ao amigo pela visita ao meu espaço e também de ter feito o comentário, pois, através dele fiquei sabendo que eu não atingi o meu objetivo de bem ensinar com facilidade pelo método do "empréstimo automático"!!!!
Em segundo lugar, quero dizer que o prezado leitor, não está errado em ensinar a subtração dessa forma, uma outra maneira e se fazer a conta da subtração entre valores!!!!
Em terceiro lugar, quero tentar lhe explicar pelo método que eu defendi na postagem como eu faria a subtração entre desses mesmos valores:
7 1
- 4 7 começamos pela 1ª ordem dos operadores...
________ de 1 eu não poso tirar 7, pois, o 1 é menor
que o 7. Daí, eu "automaticamente" adiciono
10 ao 1 (1 + 10 = 11) e agora sim, eu posso
subtrair 7 de 11 (11 - 7 = 4). Entendeu?? em toda ocasião que um algarismo no subtraendo ( o caso do 7) for maior que o algarismo acima dele no minuendo, automaticamente somamos 10 unidades ao número menor ( foi o caso do 1) e aí, fazemos como você explicou no método que usa, de 7 no subtraendo para completar o 11 (implícito no minuendo) o que faltam quatro unidades ( no inicio, antes de adicionar 10 ao 1, eu não podia falar... " 7 para 1", mas, agora eu digo... "7 para 11")!
7 1
- 4 7
________
4 continuando... a próxima subtração
seria na 2ª ordem dos operadores,
entre o 7 e o 4, podemos fazer 7 menos 4 ou... "quatro para 7" o que daria...3 ( o resultado seria ... 34??? Não!!!)!!! Mas, na subtração anterior, nós fizemos 11 menos 7, lembra-se???? E aqui está uma particularidade do método, onde, toda vez que tivermos valores no minuendo ( termo superior da subtração) somados com 10 e de sorte que efetuamos uma subtração considerando... 10, 11 (foi o que aconteceu aqui nesse exemplo. 12, 13, 14, 15, 16, 17, 18 e 19, então, vem o 1 desses números, o qual será somado com o próximo valor do número do subtraendo (esse 4 de 47)para então se fazer nova subtração. Portanto... nesse caso, o 1 de 11, desce somando ao 4 de 47 e temos... 4 + 1 = 5, de modo que, podemos fazer... 7 menos 5 e obtemos 2 ( eu digo: " 5 para 7 = 2)!!! Assim, a conta se apresentaria, com...
7 1
- 4 7
________
2 4
onde eu teria cantado um mantra (KKKKKK!!!!!)... "sete para onze faltam quatro, de onze vem um, soma com o quatro, dá cinco e... cinco para sete faltam dois"!!!!!
Gostaria que amigo, usasse o meu endereço de e-mail.... franciscovaldir61@gmail.com para dizer se agora eu pude fazê-lo entender esse processo, sim????
Obrigado, por participar e espero que faça outras visitas ao meu blog e se possível... comentando!!!!
Um abraço!!!!!
Postar um comentário